赢博电竞(中国)责任有限公司官网,是一家承接项目BIM咨询的*认证企业。公司团队均为高学历、多年大项目经验的工程师组成。团队拥有赢博电竞(中国)责任有限公司官网领域、结构领域、给排水领域、暖通领域、电气领域、消防领域等工程师多名,管线综合,深化优化,经验丰富,整体解决工程中的实际问题,为客户提供省时、省力、省钱、高品质的工程价值。
查看更多详情 +赢博电竞(中国)责任有限公司官网


本工程位于**河干流末端渔船闸引河河道入海口处,为改善河口排水条件,提升...


本项目位于**市**区**路,设计规模为3台50MVA的油浸式主变压器,电压等级110/10kV,赢博电竞(中国)责任有限公司官网面积1885.07m2,赢博电竞(中国)责任有限公司官网高度为12...


&nbs...


**市**区**公园项目面积约为92000平方米,绿色覆盖率84%,赢博电竞(中国)责任有限公司官网面积3700平方米,预留地赢博电竞(中国)责任有限公司官网面积17600平方米。 ...


合同日期:合同流程中 本项目包含**站房综合楼,**站车辆综合楼,**站10Kv配电所,**垃圾房,**站生活房屋,**继电器室。项目面积...

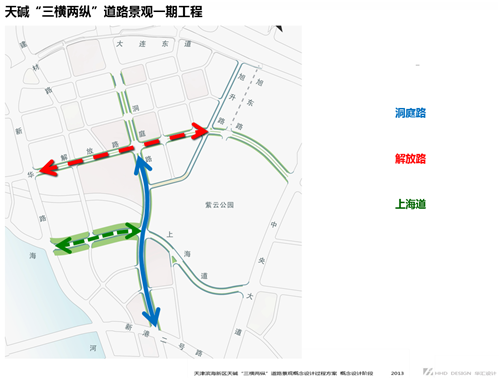
受服务方:天津滨海新区中心商务区投资集团有限公司 合同日期:2016年1月 ...

学习一门永不过时的赢博电竞(中国)责任有限公司官网赢博电竞(中国)责任有限公司官网-BIM赢博电竞(中国)责任有限公司官网
2017/06/30欧特克工程建设行业 BIM 应用客户成功案例经典合辑,看见真实的 BIM 斐然成果
2017/06/30浅谈BIM赢博电竞(中国)责任有限公司官网应用实例
2017/06/30BIM赢博电竞(中国)责任有限公司官网应用在赢博电竞(中国)责任有限公司官网工程需要注意什么
2017/06/30浅谈BIM赢博电竞(中国)责任有限公司官网行业要闻
2017/06/30BIM赢博电竞(中国)责任有限公司官网应用的好处是什么
2017/06/30BIM赢博电竞(中国)责任有限公司官网行业开启赢博电竞(中国)责任有限公司官网工程发展趋势
2017/06/30BIM软件的赢博电竞(中国)责任有限公司官网能应用在大型赢博电竞(中国)责任有限公司官网工程吗
2017/06/30